<图解算法>读书笔记
Contents
大O表示法
讨论运行时间时, log 指的都是 以2为底的log.
作用:
- 仅知道算法运行需要多长时间才能运行完毕还不够, 还需知道运行时间如何随着列表增长而增加, 这才是大O表示法的用武之地.
- 它指出了算法运行时间的增速
- 它指出的是最差情况下的运行时间
- 算法的速度指的并非时间, 而是操作数的增速(即随着输入的增加, 其运行时间将以什么样的速度增加.)
二分法查找
- 仅当列表是有序的时候, 才可以使用
书本是以 2.7 版本的代码, 我这测试的是 3.6 的代码
listdata = list(range(1, 100, 2))
def binary_search(l, element):
low = 0
high = len(l) - 1
print("total len " + str(high))
print(l)
while low <= high:
mid = int((low + high) / 2)
current = l[mid]
if current == element:
return mid
elif current < element:
low = mid + 1
else:
high = mid - 1
print("current value " + str(current) + ", mid " + str(mid) + ", low " + str(low) + ", high " + str(high))
return None
print(binary_search(listdata, 25))
线性时间
要猜测的次数与列表长度相同的, 则称为线性时间
对数时间
二分查找的运行时间就是对数时间
选择排序
log(n * 1⁄2 * n), 但大O表示法通常是省略常数的, 所以为 log(n*n) 即 log(n^2)
它适合于需要检查的元素越来越少的情况
listadata = [1, 5, 2, 9, 10, 22, 3, 99, 1000, 999, 500] def find_smallest(listdata): smallest = listdata[0] smallest_index = 0 for i in range(1, len(listadata)): if listadata[i] < smallest: smallest_index = i smallest = listadata[smallest_index] return smallest_index def select_sort(listdata): sort_list_asc = [] for i in range(len(listadata)): smallest_index = find_smallest(listdata) smallest = listdata.pop(smallest_index) sort_list_asc.append(smallest) return sort_list_asc print(select_sort(listadata))
递归
递归只是让解决方案更清晰, 并没有性能上的优势.
递归有两部分
- 基线条件 base case
递归条件 recursive case
def count_down(n): if n < 0: # 基线条件 return # 递归条件 print(n) count_down(n - 1) count_down(10)
快速排序
它使用了分而治之的策略
它的性能高度依赖基准值.
listadata = [1, 5, 2, 9, 10, 22, 3, 99, 1000, 999, 500]
def qsort(l):
if len(l) <= 1:
return l
base = l[0]
# 注意是从1: 开始, 因为我们已经选择了第0个索引为基准值
less_base_list = [i for i in l[1:] if i <= base]
greater_base_list = [i for i in l[1:] if i > base]
return qsort(less_base_list) + [base] + qsort(greater_base_list)
print(qsort(listadata))
散列函数
即无论你给它什么数据, 它都还给你一个数字. 即将输入映射到数字.
常量时间
平均 O(1) , 这意味着, 不管散列表多大, 所需的时间都相同.
最差是 O(n), 线性时间
为此需要避免散列表元素的冲突
- 较低的填装因子(= 散列表包含的元素个数/ 位置总数), 因子越低, 发生冲突的可能性就越小, 散列表的性能就越高.(因为调整的开销比较大)
- 良好的散列函数(良好的散列函数, 会让数组中的值呈均匀分布. 比如 SHA 函数)
广度优先搜索
它是一种图算法, 解决的是 最短路径 问题.
它回答了两类问题
- 从节点A出发, 有前往节点B的路径吗
- 从节点A出发, 前往节点B的哪条路径最短
图
由节点和边组成.节点之间称为 邻居 .
实现方法
- 首先将根节点放入队列中。
- 从队列中取出第一个节点,并检验它是否为目标。
- 如果找到目标,则结束搜寻并回传结果。
- 否则将它所有尚未检验过的直接子节点加入队列中。
- 若队列为空,表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。
- 重复步骤2。
若所有边的长度相等,广度优先搜索算法是最佳解——亦即它找到的第一个解,距离根节点的边数目一定最少
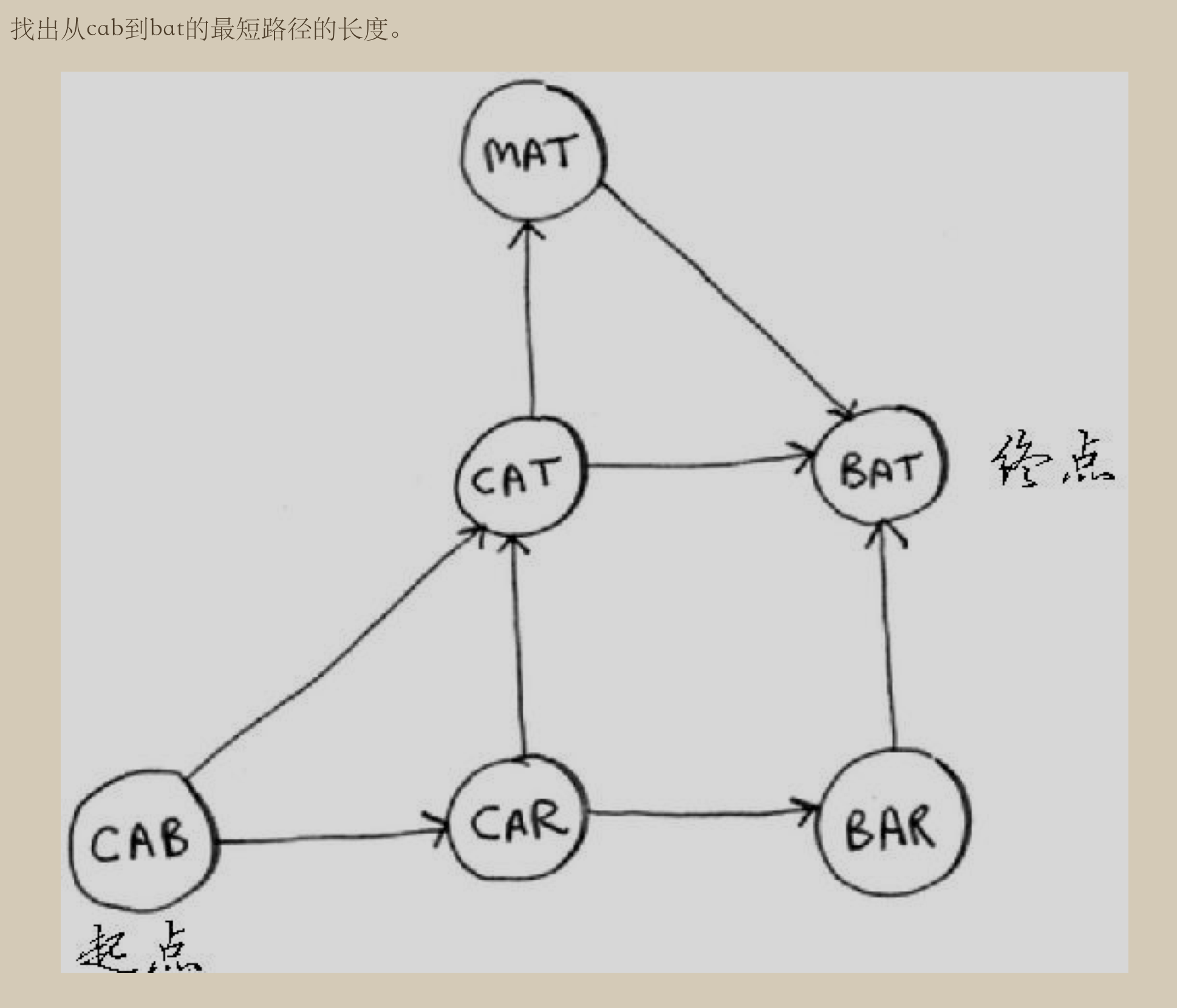
from collections import deque
graph = {}
graph['cab'] = ['cat', 'car']
graph['car'] = ['bar', 'cat']
graph['cat'] = ['bat', 'mat']
graph['mat'] = ['bat']
graph['bar'] = ['bat']
graph['bat'] = []
# 从根节点开始
start_name = 'cab'
# 已查找过的节点队列
searched = []
# 要查找的节点队列
search_queue = deque()
# 从根节点的子节点开始
search_queue += graph[start_name]
# 广度优先搜索
def search(name, search_graph):
while search_graph:
# 从队列第一个开始出队
location = search_graph.popleft()
if location not in searched:
# 找到目标节点, 则返回
if location == name:
return location
else:
# 否则将该节点的子节点, 追加到要查找的队列尾
search_graph += graph[location]
searched.append(location)
return None
# 查找父节点的名字
def find_parent(name):
for k in graph.keys():
if name in graph[k]:
return k
return name
# 打印搜索路径
def show_path(searched_queue, finded_name):
sear_path = []
cache = {}
while searched_queue:
e = searched_queue.pop(0)
p = find_parent(e)
try:
v = cache[p]
except KeyError:
cache[p] = 1
v = 0
if v == 1:
continue
sear_path.append(p)
sear_path.append(finded_name)
return sear_path
# 要查找的节点
find_name = 'bat'
# 执行查找
search(find_name, search_queue)
searched.append(find_name)
# 打印出最短路径
print("->".join(show_path(searched, find_name)))
结果为
cab->cat->bat
狄克斯特拉算法
广度优先搜索, 它可以找出段数最少的路径. 但, 如果每一段的路径耗时不同(或权重不同), 则最短的不一定是最快的. 要找出最快的路径, 则可以使用 狄克斯特拉算法.
如果有负权重, 则不适用.
算法步骤
- 找出”最便宜”的节点.
- 更新该节点的邻居开销
- 重复这个过程
计算最终路径
graph = {} graph['start'] = {} graph['start']['a'] = 6 graph['start']['b'] = 2 graph['a'] = {} graph['a']['fin'] = 1 graph['b'] = {} graph['b']['a'] = 3 graph['b']['fin'] = 5 graph['fin'] = {} infinity = float("inf") costs = {} costs['a'] = 6 costs['b'] = 2 costs['fin'] = infinity parents = {} parents['a'] = 'start' parents['b'] = 'start' parents['fin'] = None processed = [] def find_lowest_cost_node(costs): lowest_cost = float("inf") lowest_cost_node = None for node in costs: cost = costs[node] if cost < lowest_cost and node not in processed: lowest_cost = cost lowest_cost_node = node return lowest_cost_node node = find_lowest_cost_node(costs) while node is not None: cost = costs[node] neighbors = graph[node] print("neighbors => ", end=" ") print(neighbors) print("parents => ", end=" ") print(parents) for n in neighbors.keys(): new_cost = cost + neighbors[n] if costs[n] > new_cost: costs[n] = new_cost parents[n] = node processed.append(node) node = find_lowest_cost_node(costs) print("parents => ", end=" ") print(parents)
建立四个列表
- graph : 表示路径
- cost : 表示路径的消耗
- parent: 父节点.(终点的父节点, 设置为 None)
- processed: 处理过的节点
每次搜索, 都是查找最便宜的节点, 然后保存它的开销(指从起点出发, 到该节点需要多长时间)
贪婪算法
每步都采取局部最优解, 最终得到的就是全局最优解.(信不信由你.哈哈~)
教室安排
- 选出最早结束的课, 它就是要在这间教室上的第一堂课
- 选出第一堂课结束后才开始的课.同样选择结束最早的课, 这就是在这教室上的第二堂课.
- 重复以上步骤.
